2010年9月以降、Twitterはデフォルトアイコンとして卵の画像を使っています。それ以前は、鳥をかたどったものでした。
 (引用元)
(引用元)
この鳥は、円を組み合わせて作られたようで、数学的に見ても面白い形です。では、現在の卵アイコンはどうなっているのか。これもまた、数学を利用した形ではないだろうかと思い、調べてみました。

結論から述べます。Twitterのデフォルトロゴは、伊藤忠夫氏の卵形曲線方程式を利用して作られていると推定しました。山本信雄氏のホームページによれば、これは次のような形の式です。係数$a, b$は自由に決めて良いのですが、$b/a=0.78$とすることが推奨だそうです。
\[x=a cos \theta, \hspace{5mm} y=b cos \frac{\theta}{4} sin \theta \hspace{8mm}(-\pi\le \theta \le \pi) \]
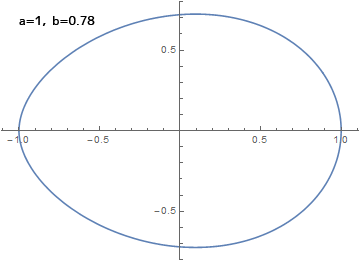
Twitterのロゴを元に、$a, b$を推定しましょう。式からわかるように、長径方向のx座標の値は明らかに$-a ~ a$の間で変化するため、まず$2a$の値がロゴの長径と等しくなる必要があります。問題は短径ですが、次のようにしてy座標値の最小・最大値を求めます。$y=b cos \frac{\theta}{4} sin \theta$を$\theta$で微分し、2倍角の公式などを次々に適用してさらに$c=cos \frac{\theta}{4}$と置くと、うまい具合に$c$だけの式になります。
\[\frac{dy}{d\theta}=10b c^5-11b c^3+2b c\]
これが0になる$c$の値は簡単に求められます。$c$の5次式方程式を解くことになりますが、全体を$bc$で割ると$c^4$と$c^2$の項しか残らず、実質的に2次方程式になるからです。途中を省略すると、解のうち$-\pi\le \theta \le \pi$を満たすのは$c=\frac{\sqrt{11+\sqrt{41}}}{2\sqrt{5}}$の場合のみ。元のy座標の式もまた2倍角の公式を使って$c$で表し、今求めた値を代入します。実に面倒くさい作業です。
\[y座標: \pm \frac{2b}{25\sqrt{5}}\sqrt{411+41\sqrt{41}}\]
これが、y座標の最大・最小値を表しているわけで、短径は$\frac{4b}{25\sqrt{5}}\sqrt{411+41\sqrt{41}}\simeq 1.85700b$となります。要するに、\[a=\frac{長径}{2}, b=\frac{短径}{1.85700}\]となるように設定すればよいわけです。
Twitterの卵アイコン画像にエッジ検出フィルターをかけて大きさを測ったところ、長径は437ピクセル、短径は317ピクセルとわかったので、$a=437/2=218.500, b=317/1.85700\simeq 170.705$と置きます。このとき、係数の比を求めると$b/a \simeq 0.781259$です。伊藤氏推奨の0.78にかなり近い比率で、卵アイコンが描かれたことがわかります。
次の図は、こうして作った曲線(赤)を卵アイコンに重ねたものです。ほぼ一致しています。

この、伊藤氏の卵形曲線方程式は、海外でも紹介されています。googleで“egg equations”を検索すると上位に登場するため、Twitterのデザイナーが参考にしていても不思議ではないように思います。そういったページを参考にした上で、$b/a=0.78$の卵を描いたのではないでしょうか。
以上のような計算を、googleで引っかかった卵形方程式について、片っ端から試しました。解析的に解くのが難しい式もあり、かなり強引な方法も使いましたが……。ともかくその結果、この伊藤氏の式が最もフィットしたというわけです。
2番目に近かったのは、伊藤氏の方程式を紹介している山本信雄氏が考えた方程式です。お二方の卵形曲線はかなり似ているため、山本氏の曲線も卵アイコンに当然近いわけですが、どちらかといえば伊藤氏の曲線の方が近いです。ただし数学的には、陰関数表示の式で次数が少なく美しいこと、媒介変数表示で変数の範囲を制限しなくても描ける(伊藤氏の式は$-\pi\le t \le \pi$の外では見当外れの場所を通る。)ことなどから、私なら山本氏の式をとります。
せっかく卵の式が得られたので、3D化してみました。
twitterEggIcon.zip(STL形式)
このファイルをDMM.makeなどに送れば、3Dプリンタで卵の実物を作ってもらえます。ちなみに3D化した卵の体積は厳密に$\frac{118}{105}\pi a b^2$と計算できました。
ここまで読んでいただいて今さらですが、アイコンをデザインした人に聞かなければ真相はわかりません。そのため、ブログ記事のタイトルには(?)を付けました。単に卵の写真をベジエ曲線でなぞっただけ、というつまらない結論もあり得ます。どなたか確かめてくれると嬉しいのですが……。

最近のコメント