頒布した同人誌に下記の誤りがあったためお知らせします。
| ページ・場所 | 訂正前 | 訂正後 |
|---|---|---|
| P 8 脚注1 | ヨーロッパでは結婚は大半は | ヨーロッパでは、結婚の大半は |
| P 8 下段最後から5行目 | 私とと彼らは | 私と彼らは |
| P27 上段最後から7行目 | 作り上げてた | 作り上げた |
| P32 下段2行目 | どの部屋に入ってて | どの部屋に入って |
| P40 上段9行目 | モデルを2台を作った | モデルを2台作った |

頒布した同人誌に下記の誤りがあったためお知らせします。
| ページ・場所 | 訂正前 | 訂正後 |
|---|---|---|
| P 8 脚注1 | ヨーロッパでは結婚は大半は | ヨーロッパでは、結婚の大半は |
| P 8 下段最後から5行目 | 私とと彼らは | 私と彼らは |
| P27 上段最後から7行目 | 作り上げてた | 作り上げた |
| P32 下段2行目 | どの部屋に入ってて | どの部屋に入って |
| P40 上段9行目 | モデルを2台を作った | モデルを2台作った |
タイトルの通りです。2023/5/21(日)、10年以上振りとなります。前回と比較すると、訳文の見直しはもちろん、中に書かれている情報についても最近判明したことを反映させ、大幅にアップデートしています。詳しくは文学フリマ東京36のカタログをご覧ください。

クルタ計算機の解説マニュアル”Computing Examples for the Curta Calculating Machine.”の日本語翻訳版が、発笑探検隊(3日目 東2-S28a, http://takuri.realwork.jp/, @takuri_east)によりC92で頒布されます。私が関わるクルタ本では、開発者自伝本、”YOUR CURTA CALCULATOR”翻訳本に続く3冊目となります。
今回は、機械式計算機による超絶テクニックを紹介する本です。機械式計算機全盛期には、計算機の限界ゆえにかなり高等な計算法が用いられていました。この本でその一部を感じられるかと思います。少し中身を紹介します。 続きを読む
かなり間が空きましたが、『スラックラインの数理』2回目です。今回は、実際にスラックラインを張るときに役立つかもしれない話題、ラインの張力と沈み込み量の関係を見てみたいと思います。沈み込み量とは、ラインに人が乗ったときにラインと足の接点が元の高さから下がる長さです。足とラインの接点は、この沈み込み量を半径とする円周上で揺れるので、この量が変わると乗り心地が全然異なります。一般的に、沈み込み量が大きいほど慣れるのに時間がかかりますが、小さい場合もそれはそれで特有の難しさがあるのでどちらが難しいというわけではなく、とにかく感覚が全然違うとしか言いようがありません。
スラックライン業界ではすでに知られた式があって、例えばスラックラインの歩き方さんのホームページではその計算フォームも公開されています。今回は、これよりももう少し踏み込んだ分析をやってみますが、とりあえずはこの式を導きましょう。
「素数の出方はランダムではなかった。1億個調べて浮かんだ奇妙な数」という記事があったので、Mathematicaで確認してみました。まず100万番目までの素数を求め、素数とその次の素数の間で末尾がどう変化するかの遷移行列を作ります。一桁の素数は末尾が特異なので、外しました。
n = 1000000;
primes = Table[Prime[i], {i, 5, n}];
pairs = Table[{Prime[i], Prime[i + 1]}, {i, 5, n}];
mat = Map[Normalize[#, Total] &,
Table[Cases[Mod[pairs, 10], {i, j}] //
Length, {i, {1, 3, 7, 9}}, {j, {1, 3, 7, 9}}] // N];
mat // MatrixFormMatrixPlot[mat, FrameTicks -> {{{1, 1}, {2, 3}, {3, 7}, {4, 9}}, {{1, 1}, {2, 3}, {3,7}, {4, 9}}}]
重力波検出のニュースが話題ですが、その波形生データが公開されていたのでMathematica で分析してみました。取り扱うのは4096Hzでサンプリングされた4096秒分×測定値2箇所分(Hanford, Livingston)のHDF5形式データです。(他に16384Hzのデータ、32秒分のデータがあるので、測定地点×サンプリング周波数×測定時間で計8通りのデータが載っています。)
分析するには、理論上どんな波形が検出されるかを知っておいたほうが有利です。今回は都合良く、2つのブラックホールが衝突した時の理論曲線が公開されています。
sr = 4096;
template = Partition[ToExpression[StringReplace[StringSplit[Import[“https://losc.ligo.org/s/events/GW150914/GW150914_4_NR_waveform.txt”]], “e” -> “*^”]], 2];
template2 = #[[2]] & /@ template;
ListLinePlot[template2]
これが観測データに含まれているはずなので、パターンマッチングで見つければ良いわけです。波形でパターンマッチングと言えば相互相関関数ですかね。相互相関関数とは、観測データからパターンと同じ秒数分を取り出して、かけ算して積分(つまり内積)した値を並べた関数です。パターンの長さをTp秒、観測データの長さをT秒とすると、まず観測データの0~Tp秒分を取り出して積分を計算し、これを少しずつずらしながら最後はT-Tp~T秒分の積分値まで計算します。するとTからTp秒分だけ少なくなった一連の積分値が得られるのですが、これを関数と見なすわけです。波形の大きさを正規化しておけば、パターンと完全に一致している箇所では1に、似ていないほど0に近くなり、パターンと完全に正負が逆転した箇所では-1になります。観測データとパターンを相互相関関数でつきあわせてみましょう。
dataH = Import[“https://losc.ligo.org/s/events/GW150914/H-H1_LOSC_4_V1-1126257414-4096.hdf5”, {“Datasets”, “/strain/Strain”}];
dataL = Import[“https://losc.ligo.org/s/events/GW150914/L-L1_LOSC_4_V1-1126257414-4096.hdf5”, {“Datasets”, “/strain/Strain”}];corH = ListCorrelate[template2, dataH]/Sqrt[MovingAverage[dataH^2, Length[template2]] Length[template2] Total[template2^2]];
posH = Position[corH, Max[corH]][[1, 1]]
corL = ListCorrelate[template2, dataL]/Sqrt[MovingAverage[dataL^2, Length[template2]] Length[template2] Total[template2^2]];
posL = Position[corL, Min[corL]][[1, 1]]ListLinePlot[Downsample[corH, 10], PlotRange->All
ListLinePlot[Downsample[corL, 10], PlotRange->All]
さすがに、生データからは何も読み取れませんでした。(最初にピークがありますが、端点なので処理上異常値が出ているようです。)そこで観測データに何らかの処理をしなければならないわけですが、今回必要なことはある一瞬の変化を際立たせることで、逆に言えばデータ全体にまんべんなく入っているような動きは抑え込まなくてはなりません。これにはホワイトニングという手法を使います。一番簡単なのは、観測データをフーリエ変換して各周波数の成分(複素数)を求め、その絶対値で割り算し、フーリエ逆変換で元に戻すという方法です。これにより、観測データ全体に入っているような周波数ほど抑えられ、局地的にしか入っていないデータが強調されることになります。
dataHwhitened = InverseFourier[Fourier[dataH]/(Fourier[dataH] // Abs)] // Chop;
dataLwhitened = InverseFourier[Fourier[dataL]/(Fourier[dataL] // Abs)] // Chop;
これで、観測データの見かけはホワイトノイズになりました。これをもしフーリエ変換したら、全周波数で同じ強度のパワースペクトルが得られるはずです。このデータで相互相関関数を作ってみます。先ほどとほぼ同じコードです。
corH = ListCorrelate[template2, dataHwhitened]/Sqrt[MovingAverage[dataHwhitened^2, Length[template2]] Length[template2] Total[template2^2]];
posH = Position[corH, Max[corH]][[1, 1]]
corL = ListCorrelate[template2, dataLwhitened]/Sqrt[MovingAverage[dataLwhitened^2, Length[template2]] Length[template2] Total[template2^2]];
posL = Position[corL, Min[corL]][[1, 1]]ListLinePlot[Downsample[corH, 10], PlotRange->All]
ListLinePlot[Downsample[corL, 10], PlotRange->All]
これで、明確に検出されました。実は2つのデータでピーク位置がデータ 29個分(7ms)だけずれているのですが、これは観測地が離れているために重力波の到達時刻が異なったのが原因です。観測所同士は約10ミリ光秒だけ離れているので、(重力波の進行速度が光と同じだと仮定すると)重力波が斜めに入ってきたことがわかります。これを元に、ある程度重力波源の位置を絞れるのでしょう。
この相関関数のヒストグラムを描くと、正規分布にかなり近いように見えます。(±1の範囲しか動かないので厳密に正規分布ではありません。)
正規分布だと仮定すると、信号位置のピークは10.93σと8.16σとなり、かなり強く検出されたように思われます。2箇所の観測データを突き合わせて、例えば0.05秒以内に2つのデータが6σ以上を閾値とすると、誤検知はもっと抑えられるのではないでしょうか。
(上の時系列グラフはダウンサンプリングしているので、本当のピーク値はもう少し大きい)
検出された付近の波形を見てみます。ピーク部分の観測データを、正規化してパターンと重ね合わせてみました。また、ピークが負だった方のデータはパターンと逆転しているということですから、正負を逆転させています。
ListLinePlot[
Normalize /@ {template2[[Floor[Length[template2] 8/10] ;; Length[template2]]], dataHwhitened[[posH + Floor[Length[template2] 8/10] ;; posH + Length[template2]]],-dataLwhitened[[posL + Floor[Length[template2] 8/10] ;; posL + Length[template2]]]}, PlotRange -> All]
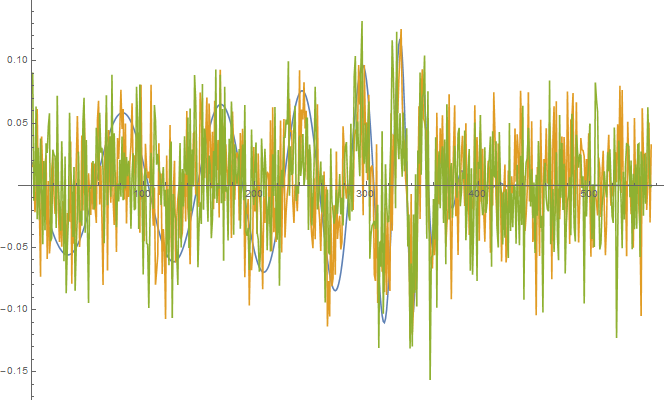 高周波のノイズがまだ残っていて、わかりにくいですね。データから10~280Hzの部分だけを取り出してみます。
高周波のノイズがまだ残っていて、わかりにくいですね。データから10~280Hzの部分だけを取り出してみます。
dataHfiltered =BandpassFilter[dataHwhitened, {10, 280} 2 Pi, 300, HammingWindow,SampleRate -> sr];
dataLfiltered =BandpassFilter[dataLwhitened, {10, 280} 2 Pi, 300, HammingWindow,SampleRate -> sr];
ListLinePlot[Normalize /@ {template2[[Floor[Length[template2] 8/10] ;; Length[template2]]],
dataHfiltered[[posH + Floor[Length[template2] 8/10] ;; posH + Length[template2]]],
-dataLfiltered[[posL + Floor[Length[template2] 8/10] ;;posL + Length[template2]]]}, PlotRange -> All]
かなり良い感じではないでしょうか。というわけで、家庭のコンピュータでも重力波検出は一応可能でした。ただ実際には、もっと多くのパターンとの照合や、突発的なノイズ(地震、周囲の交通、風など)への対応が必要なのでしょう。
最近、スラックラインを練習しています。スラックラインとは、綱渡りのようなもの、というかほとんど綱渡りそのものをスポーツにしたもので、綱渡りとの違いは
といったところです。で、これのコツは足を少し曲げて重心を低くすることなんですね。実際、足を曲げると安定します。しかしこれっておかしくないですかね?
いや、だって倒立振子とかでは重心位置が高い方が安定するじゃないですか。登山でも、重いものはザックの上に来るように配置しろと言われるじゃないですか。不思議だ、というわけでモデルを作って分析してみました。
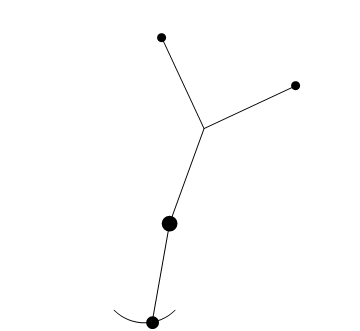 続きを読む
続きを読む
iPhoneは3軸の加速度計を内蔵しています。iPhoneの本体を傾けると画面が縦モードになったり横モードになったりしますが、あれは加速度計で重力方向を検出して、向きを検知しているわけです。しかしせっかく加速度計があるので、もっといろいろな応用、例えば震度計としても使えるのではないでしょうか。そこで、夏休みの自由研究として、iPhoneの加速度計で地震の震度を計ってみました。そして、気象庁がどうやって震度を決めているのかも調べました。
とは言うものの、地震が来るまで待ってはいられません。運が良いことに、防災行事で起震車に乗る機会があったので、iPhoneのSensorLogというアプリで地震発生から終了までの加速度を計測してみました。震度7の揺れです。
2010年9月以降、Twitterはデフォルトアイコンとして卵の画像を使っています。それ以前は、鳥をかたどったものでした。
 (引用元)
(引用元)
この鳥は、円を組み合わせて作られたようで、数学的に見ても面白い形です。では、現在の卵アイコンはどうなっているのか。これもまた、数学を利用した形ではないだろうかと思い、調べてみました。

結論から述べます。Twitterのデフォルトロゴは、伊藤忠夫氏の卵形曲線方程式を利用して作られていると推定しました。山本信雄氏のホームページによれば、これは次のような形の式です。係数$a, b$は自由に決めて良いのですが、$b/a=0.78$とすることが推奨だそうです。
\[x=a cos \theta, \hspace{5mm} y=b cos \frac{\theta}{4} sin \theta \hspace{8mm}(-\pi\le \theta \le \pi) \]
続きを読む
最近のコメント