かなり間が空きましたが、『スラックラインの数理』2回目です。今回は、実際にスラックラインを張るときに役立つかもしれない話題、ラインの張力と沈み込み量の関係を見てみたいと思います。沈み込み量とは、ラインに人が乗ったときにラインと足の接点が元の高さから下がる長さです。足とラインの接点は、この沈み込み量を半径とする円周上で揺れるので、この量が変わると乗り心地が全然異なります。一般的に、沈み込み量が大きいほど慣れるのに時間がかかりますが、小さい場合もそれはそれで特有の難しさがあるのでどちらが難しいというわけではなく、とにかく感覚が全然違うとしか言いようがありません。
スラックライン業界ではすでに知られた式があって、例えばスラックラインの歩き方さんのホームページではその計算フォームも公開されています。今回は、これよりももう少し踏み込んだ分析をやってみますが、とりあえずはこの式を導きましょう。
数式が多いのでMathJaXを使用します。古いブラウザでは読めないかもしれません。
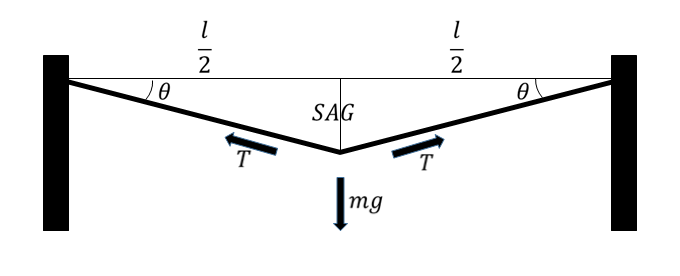
ラインの中央に乗った場合を考えて、各変数を上図のように設定します。つまり、
$T$:ラインの張力 $\theta$:ラインの傾き角 $SAG$:沈み込み量 $m$:体重 $g$:重力加速度
です。$SAG$は、英語で「たわみ」を意味する単語で、スラックライン界隈ではよく使われるようです。この問題は、高校で習った物理の範囲で解けます。
\[2T sin \theta = m g(縦の力が釣り合っている。)\]
\[ \frac{l}{2} \tan \theta = SAG(幾何学的事実) \]
この2式から$\theta$を消去します。解き方はいろいろとありますが、$\sin^{2}\theta =\frac{\tan^{2} \theta}{1+\tan^{2}\theta}$の公式を使うのが良いかもしれません。結果的にこうなります。
\[ m^2 g^2 (l^2 +4 SAG^2 )=16 SAG^2 T^2 \]
これを使うと、張力から沈み込み量、またその逆を計算できます。
\[ SAG=\frac{m g l}{2 \sqrt{4 T^2 -m^2 g^2}} \]
\[ T = \frac{m g \sqrt{l^2+4SAG^2}}{4 SAG} \]
2番目の式において$SAG\ll l$なので、$\sqrt{l^2+4SAG^2}$を$l$と近似すると
\[T \simeq \frac{m g l}{4 SAG}\]
となり、(記号が違いますが)上のホームページで紹介された式になります。深く沈み込むように張った場合は、この近似がなり立たなくなるので厳密な式を使った方が良いでしょう。
次に、ラインの伸縮を考慮した計算式を作ってみます。上の式では張力を$T$としましたが、この$T$はあくまでもラインに人が乗った場合の張力で、セットアップ時の張力よりも当然増えています。それがどれぐらい増えるのか、あるいは別の体重の人が乗ったらどうなるのか、トリックをやりやすいのはどんなラインかなどを分析するためには、ラインの伸縮力を考えなくてはなりません。
一般的に、バネなどは与えた力に比例した長さだけ長くなるので、その仮定を用いましょう。$T$ の力を掛けた時に、ラインの長さが$1+k T$倍になると設定します。この$k$の値がどの程度になるのかはなかなかわからないのですが、ここに複数製品で実験した結果が載っています。残念ながら力と伸びが比例関係から外れているように見えますが、とりあえずは$k$で比例するとしたまま進めましょう。グラフを見ると、堅い材質のものは大体10kNで5%、柔らかい材質のものは15%ほど伸びるようです。すなわち、$k=0.05/10000 \sim 0.15/10000$(単位は1/N)というわけです。
ラインを張った時の張力を$T_0$とします。そして上に人が乗って張力が$T$になったと仮定して、その前後でどの程度ラインが伸びたかを、$k$を元に計算します。張力0の時に比べて$T_0$を掛けた時の長さが$(1+k T_0)$倍、$T$を掛けた時の長さが$(1+k T)$倍ですから、人が乗ると$(1+k T)/(1+k T_0)$倍になったことになります。上の設定では人が乗ったときのラインの長さは$2\sqrt{(\frac{l}{2})^2 +SAG^2}$となるので、これが$l \cdot \frac{1+k T}{1+k T_0}$に等しいはずです。
つまり、
\[\left(l\cdot\frac{1+k T}{1+k T_0}\right)^2=4\left\{ \left(\frac{l}{2}\right)^2 +SAG^2\right\}\]
となり、これと先ほどの
\[m^2 g^2 (l^2 +4 SAG^2 )=16 SAG^2 T^2\]
から頑張って$T$を消去すると次のような方程式になります。
\[
64(k T_0+1)^2 SAG^4-32(k T_0+1)m g k l SAG^3\\+4 k l^2(m^2 g^2 k+4 k {T_0}^2+8 T_0)SAG^2\\-8 m g k l ^3(k T_0+1)SAG+m^2 g^2 k^2 l^4=0\]
この式を$SAG$で解けば、体重から沈み込み量を計算できます。とは言うものの、4次方程式です。1変数の方程式は4次以下ならば一応代数的に解けますが、結果はかなり複雑な式になってしまいます。

こんな感じなので、ニュートン法などで数値計算したほうが楽かもしれません。
こういう面倒な計算をやり始めた理由は、前から疑問だったことがあるからで、それは「堅いラインと柔らかいラインではどう違うのだろうか」です。もちろんラインの堅さが違えば乗り心地が違うのは当然ですが、柔らかいラインも高い張力で設置すれば堅いラインと同じことでは?と疑問を持っていたわけです。そこで、堅さが5%/10KNと15%/10KNの10mラインについて、体重70kgの人が乗った時の沈み込み量が同じになるように張力を調整し、その後に体重を変化させて$SAG$がどのように変化するかを計算してみました。
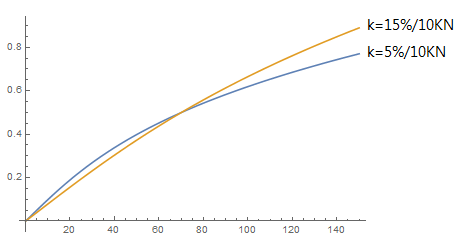
これを見ると、柔らかいラインは堅いラインに比べて体重付近での$SAG$の傾きが大きい、つまり僅かな力変化で位置が変化する、簡単に言えば縦に揺れやすいことがわかります。初心者にとっては、ただでさえ横に揺れるスラックラインが縦にも揺れて難易度が増してしまいます。逆にバットバウンスなどを練習する場合は、深く沈み込む柔らかいラインのほうがおしりが痛くなくて済み、やりやすいかもしれません。ただ、堅さが3倍も違うのに差はこの程度しかないというのは、個人的に意外でした。これぐらいなら、先ほどのページで見えた非線形性の影響のほうが大きいはずで、やはり単純なモデルでは分析に限界があるのかもしれません。
次に、ライン上を歩いて行く際に$SAG$がどのように変化するかを解明します。ラインを端から渡ると、はじめは$SAG$が小さくて揺れにくく、中央付近では$SAG$が大きくなって揺れやすく、反対側の端に着くとまた戻ります。これが再現できるでしょうか。下図のように記号を決めます。
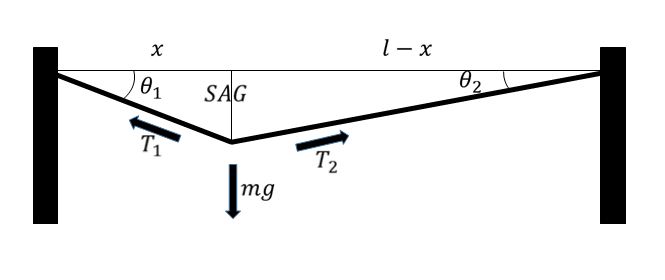
方程式をこう立ててみました。
\[T_1 \sin \theta_1+T_2 \sin \theta_2=m g (縦の力が釣り合っている。)\]
\[T_1 \cos \theta_1=T_2 \cos \theta_2 (横の力が釣り合っている。)\]
\[x \tan\theta_1=SAG (幾何学的事実)\]
\[(l-x)\tan\theta_2=SAG (幾何学的事実)\]
\[\frac{SAG}{\sin\theta_1}\frac{1+k T_0}{1+k T_1}+\frac{SAG}{\sin\theta_2}\frac{1+k T_0}{1+k T_2}=l (伸びたラインの張力をT_0に戻すと長さlになる。)\]
方程式が5本なので、未知数が5個まで許されます。$T_1, T_2, \theta_1, \theta_2, SAG$を未知数とし、$SAG$以外の4変数を消去するとこうなります。数式処理ソフトを使っても大変でした。
\[\frac{1}{\frac{m g k (l-x)}{l SAG}+\frac{1}{\sqrt{SAG^2+x^2}}}+\frac{1}{\frac{m g k x}{l
SAG}+\frac{1}{\sqrt{(l-x)^2+SAG^2}}}=\frac{l}{k T_0+1}\]
これは、代数的に解くのは無理ではないかと思います。そこで数値計算により、$x=0\sim x=l$まで変化させた時の$SAG$の軌跡を描きました。つまり、足とラインの接点を空間上に描くとこういう軌跡になるという図です。(さきほどの柔らかいラインで計算し、$SAG$に-1を掛けて反転させています。)

当たり前ですが、ラインの真ん中ほど深く沈み込み端に近づくほど浅くなるというグラフになりました。ただ個人的には、ある程度中のほうに来たらそれほど沈み込み量は変わらないと感じていたため、中心部付近でも意外に変化があるなという印象です。
ちなみに、$SAG$さえわかれば張力$T_1,T_2$は次のように計算できます。この2つの張力は、ちょうどラインの中間地点でもない限り等しくありません。
\[ T_1=\frac{m g (l-x) \sqrt{\text{SAG}^2+x^2}}{l \text{SAG}} \]
\[ T_2=\frac{m g x \sqrt{l^2-2 l x+\text{SAG}^2+x^2}}{l \text{SAG}}\]
今回は、ライン上での感覚が$SAG$によってのみ決まるという前提で見てきましたが、実際には例えば「長いラインの端のほう」と「短いラインの真ん中」では、$SAG$が同じでも何かが違うように感じます。$SAG$以外にも難易度を決める何らかのパラメータがあるような気がするので、また何かがわかったら書く予定です。

最近のコメント