「素数の出方はランダムではなかった。1億個調べて浮かんだ奇妙な数」という記事があったので、Mathematicaで確認してみました。まず100万番目までの素数を求め、素数とその次の素数の間で末尾がどう変化するかの遷移行列を作ります。一桁の素数は末尾が特異なので、外しました。
n = 1000000;
primes = Table[Prime[i], {i, 5, n}];
pairs = Table[{Prime[i], Prime[i + 1]}, {i, 5, n}];
mat = Map[Normalize[#, Total] &,
Table[Cases[Mod[pairs, 10], {i, j}] //
Length, {i, {1, 3, 7, 9}}, {j, {1, 3, 7, 9}}] // N];
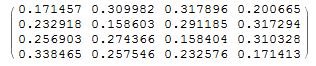
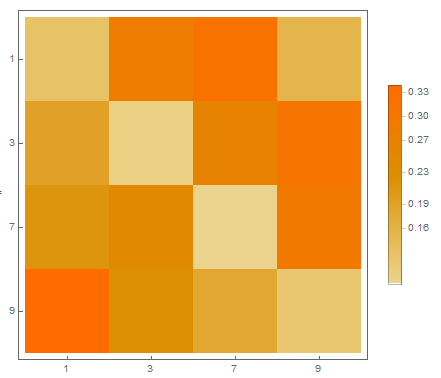
mat // MatrixFormMatrixPlot[mat, FrameTicks -> {{{1, 1}, {2, 3}, {3, 7}, {4, 9}}, {{1, 1}, {2, 3}, {3,7}, {4, 9}}}]
10以上の素数は末尾が1, 3, 7, 9のみなので4×4の行列を作りました。例えば行列の右上の数字0.200665は、末尾が1の素数の次に末尾が9の素数が来る確率が0.200665であることを示しています。つまり、同じ末尾が連続する確率は対角線上を見ればわかるわけで、確かに他に比べて値が小さいことがわかります。もし隣り合う素数同士が完全に無相関なら、この行列はすべて0.25になるはずです。
末尾の分布だけを見るとほぼ均衡に分布しているので、ますます不思議です。
Histogram[Mod[primes, 10], {1}]
この原因を探るために、隣り合う素数間の差の分布を取ってみました。
Histogram[#[[2]]- #[[1]] & /@ pairs, {1}]
素数同士ですから、差は必ず2の倍数になります。このうち10の倍数のところが、末尾が同じ素数が続いているケースとなります。分布グラフから2つのことがわかります。
- 全体的に見て、差が大きくなるほどその頻度が下がる。
- ただし、差が6の倍数である場合、周囲に比べると頻度が高い。
前者は、2つの数字の差が大きいほどその間に素数が入り込んでくる可能性が高くなるので、当然と言えます。後者は、6が2でも3でも割り切れることが原因かと思います。非素数のうち2または3で割り切れる数は、6を足しても同じ性質を持ちます。逆に素数についても、6の倍数を足しても、少なくとも2の倍数でも3の倍数でもないので、素数のままでいる可能性が相対的に高いのではないかと想像できます。
そうすると素数間の差の頻度が周囲よりも高いのは6, 12, 18, 24, 30,…ということになるのですが、末尾だけを見ると0は他の2,4,6,8が出現した後にやっと現れます。つまり末尾が変わらない0のケースは、この「6の倍数効果」を頻度がかなり低くなった時点でしか受けられないため、他の場合よりも発生しにくいのではないでしょうか。また、グラフの横軸は2,4,6,8,10,12,…となっていて末尾0は他の数字よりも後に現れるため、全体的に右下がりのグラフでは10の倍数は不利になることも言えるでしょう。
いやいや、10の倍数だって2でも5でも割り切れるので「10の倍数効果」もあるんじゃないか?確かにその通りなのですが、6の倍数よりも効果がより弱いのですね。10の倍数を足すと3を法とした値が変わるので、3で割り切れて非素数になってしまう確率がかなりあるわけです。
従って隣り合う素数同士を比較すると末尾が同じ確率が小さくなっているのではないか、そう推定するのですがどうでしょうか。
追記(2016.3.18)
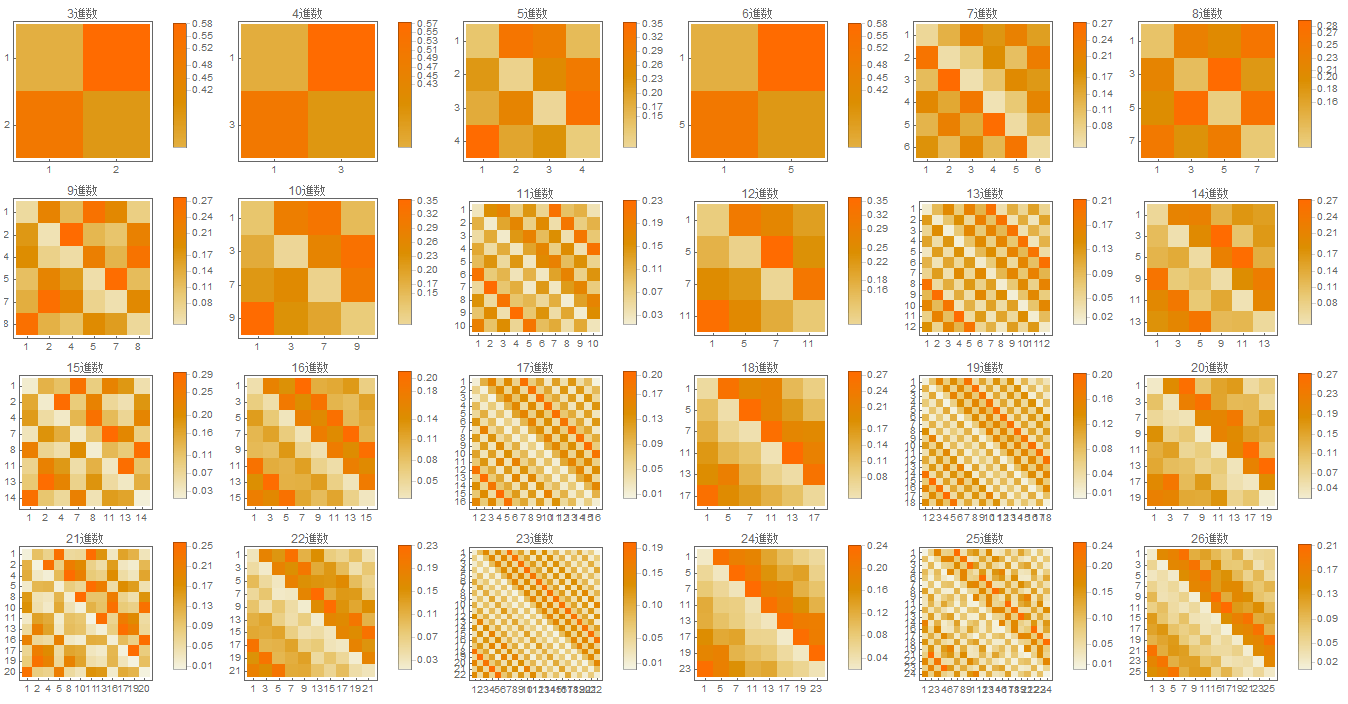
少し気になることがあったので、素数を10進数以外で表した場合に末尾がどうなるかを調べてみました。3~26進数で末尾の遷移行列を描いてみたのがこれです。(2016.3.20 次図の目盛りが間違っていたので差し替えました。)
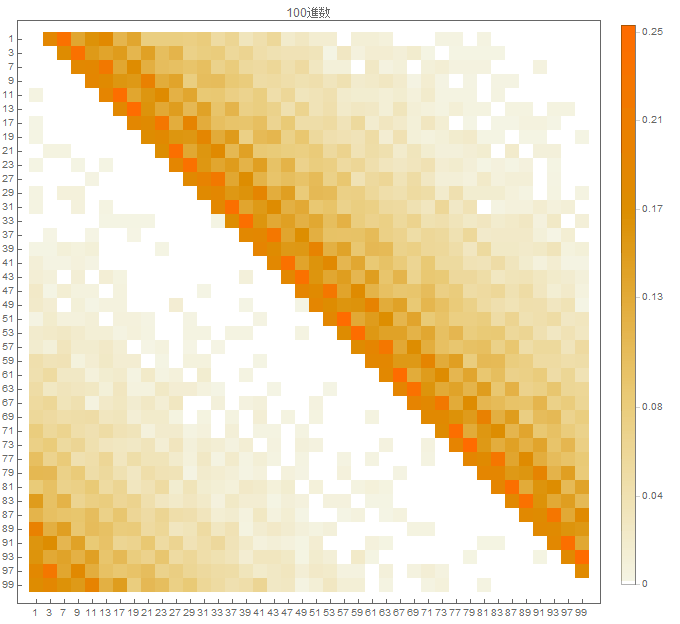
どの進数でも、末尾が連続する頻度は低く(対角線が白く)なっていることがわかります。さらに極端な場合として、100進数でのグラフを描くとこうなります。
対角線の頻度はもちろん低いのですが、その右(上)は一番濃く、これは素数間が2+100n(もちろん大半はn=0)離れたケースとなります。素数間が離れるほど(右上に行くほど)徐々に薄くなっています。
100進数では、末尾が変わらないのは素数間がちょうど100の倍数だけ離れている場合なので、100n+2や100n+4(n=0,1,…) 離れているより珍しいのは当たり前です。でもこれ、10進数でも同じ現象が起きているはずです。ちょうど10離れた素数の組み合わせは2や4離れたものより少ない。ただし8だけ離れた素数は多いようですが、18離れた素数が20離れた素数よりもかなり少なく、全体として見ると10の倍数離れた素数同士は他よりも珍しくなっています。これが、隣り合う素数で末尾が同じケースが少ないことの理由かと思います。
上で書いた「6の倍数効果」はあまり意味が無く、むしろサブの理由だと思っていた
「グラフの横軸は2,4,6,8,10,12,…となっていて末尾0は他の数字よりも後に現れるため、全体的に右下がりのグラフでは10の倍数は不利」
が本質的なのでしょう。つまり、隣り合う数字の間隔が長くなるほど頻度が落ちるような数列、例えばある数字が含まれるかどうかが一定の確率で決まるような数列ならば、同じ性質を持つはずです。ある一定規模以上の大地震が発生した年の数列なんかでも、なり立つのではないでしょうか。あまり素数の性質とは関係なく、ましてや素数の神秘性云々とも無縁だという、意外な結論になりました。

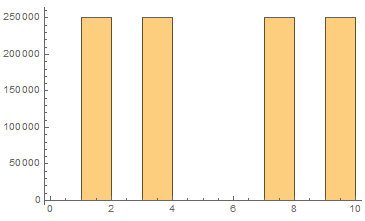
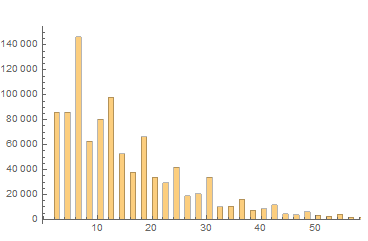
2 個のコメント
6進数の図は5?
Author
ああああ、目盛の数字が間違っていました。具体的に言えば、MathematicaのFrameTicksの使い方を間違えていました。
お恥ずかしい。ご指摘ありがとうございます。差し替えました。