Mathematicaで重力波データを解析

重力波検出のニュースが話題ですが、その波形生データが公開されていたのでMathematica で分析してみました。取り扱うのは4096Hzでサンプリングされた4096秒分×測定値2箇所分(Hanford, Livingston)のHDF5形式データです。（他に16384Hzのデータ、32秒分のデータがあるので、測定地点×サンプリング周波数×測定時間で計8通りのデータが載っています。）

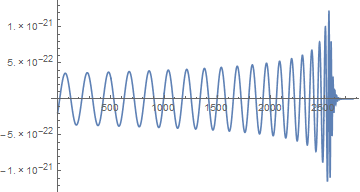
分析するには、理論上どんな波形が検出されるかを知っておいたほうが有利です。今回は都合良く、2つのブラックホールが衝突した時の理論曲線が公開されています。

sr = 4096;
template =   Partition[ToExpression[StringReplace[StringSplit[Import[“https://losc.ligo.org/s/events/GW150914/GW150914_4_NR_waveform.txt”]], “e” -> “*^”]], 2];
template2 = #[[2]] & /@ template;
ListLinePlot[template2]

これが観測データに含まれているはずなので、パターンマッチングで見つければ良いわけです。波形でパターンマッチングと言えば相互相関関数ですかね。相互相関関数とは、観測データからパターンと同じ秒数分を取り出して、かけ算して積分（つまり内積）した値を並べた関数です。パターンの長さをTp秒、観測データの長さをT秒とすると、まず観測データの0～Tp秒分を取り出して積分を計算し、これを少しずつずらしながら最後はT-Tp～T秒分の積分値まで計算します。するとTからTp秒分だけ少なくなった一連の積分値が得られるのですが、これを関数と見なすわけです。波形の大きさを正規化しておけば、パターンと完全に一致している箇所では1に、似ていないほど0に近くなり、パターンと完全に正負が逆転した箇所では-1になります。観測データとパターンを相互相関関数でつきあわせてみましょう。

dataH = Import[“https://losc.ligo.org/s/events/GW150914/H-H1_LOSC_4_V1-1126257414-4096.hdf5”, {“Datasets”, “/strain/Strain”}];
dataL = Import[“https://losc.ligo.org/s/events/GW150914/L-L1_LOSC_4_V1-1126257414-4096.hdf5”, {“Datasets”, “/strain/Strain”}];

corH = ListCorrelate[template2, dataH]/Sqrt[MovingAverage[dataH^2, Length[template2]] Length[template2] Total[template2^2]];
posH = Position[corH, Max[corH]][[1, 1]]
corL = ListCorrelate[template2, dataL]/Sqrt[MovingAverage[dataL^2, Length[template2]] Length[template2] Total[template2^2]];
posL = Position[corL, Min[corL]][[1, 1]]

ListLinePlot[Downsample[corH, 10], PlotRange->All
ListLinePlot[Downsample[corL, 10], PlotRange->All]

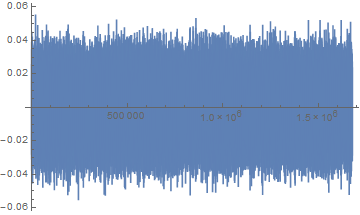
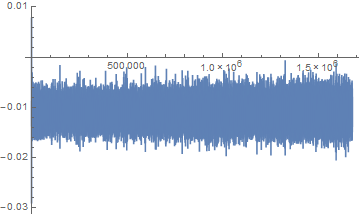
さすがに、生データからは何も読み取れませんでした。（最初にピークがありますが、端点なので処理上異常値が出ているようです。）そこで観測データに何らかの処理をしなければならないわけですが、今回必要なことはある一瞬の変化を際立たせることで、逆に言えばデータ全体にまんべんなく入っているような動きは抑え込まなくてはなりません。これにはホワイトニングという手法を使います。一番簡単なのは、観測データをフーリエ変換して各周波数の成分（複素数）を求め、その絶対値で割り算し、フーリエ逆変換で元に戻すという方法です。これにより、観測データ全体に入っているような周波数ほど抑えられ、局地的にしか入っていないデータが強調されることになります。

dataHwhitened =   InverseFourier[Fourier[dataH]/(Fourier[dataH] // Abs)] // Chop;
dataLwhitened =   InverseFourier[Fourier[dataL]/(Fourier[dataL] // Abs)] // Chop;

これで、観測データの見かけはホワイトノイズになりました。これをもしフーリエ変換したら、全周波数で同じ強度のパワースペクトルが得られるはずです。このデータで相互相関関数を作ってみます。先ほどとほぼ同じコードです。

corH = ListCorrelate[template2, dataHwhitened]/Sqrt[MovingAverage[dataHwhitened^2, Length[template2]] Length[template2] Total[template2^2]];
posH = Position[corH, Max[corH]][[1, 1]]
corL = ListCorrelate[template2, dataLwhitened]/Sqrt[MovingAverage[dataLwhitened^2, Length[template2]] Length[template2] Total[template2^2]];
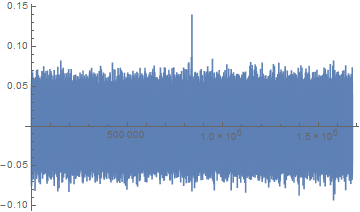
posL = Position[corL, Min[corL]][[1, 1]]

ListLinePlot[Downsample[corH, 10], PlotRange->All]
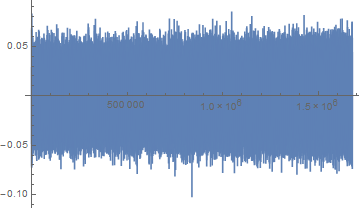
ListLinePlot[Downsample[corL, 10], PlotRange->All]

これで、明確に検出されました。実は2つのデータでピーク位置がデータ 29個分(7ms)だけずれているのですが、これは観測地が離れているために重力波の到達時刻が異なったのが原因です。観測所同士は約10ミリ光秒だけ離れているので、（重力波の進行速度が光と同じだと仮定すると）重力波が斜めに入ってきたことがわかります。これを元に、ある程度重力波源の位置を絞れるのでしょう。

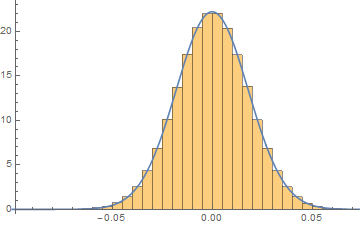
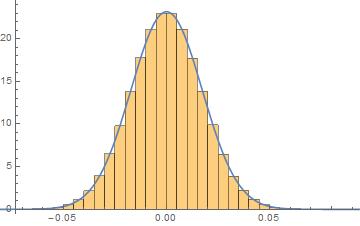
この相関関数のヒストグラムを描くと、正規分布にかなり近いように見えます。（±1の範囲しか動かないので厳密に正規分布ではありません。）

正規分布だと仮定すると、信号位置のピークは10.93σと8.16σとなり、かなり強く検出されたように思われます。2箇所の観測データを突き合わせて、例えば0.05秒以内に2つのデータが6σ以上を閾値とすると、誤検知はもっと抑えられるのではないでしょうか。

(上の時系列グラフはダウンサンプリングしているので、本当のピーク値はもう少し大きい)

検出された付近の波形を見てみます。ピーク部分の観測データを、正規化してパターンと重ね合わせてみました。また、ピークが負だった方のデータはパターンと逆転しているということですから、正負を逆転させています。

ListLinePlot[
Normalize /@ {template2[[Floor[Length[template2] 8/10] ;; Length[template2]]], dataHwhitened[[posH + Floor[Length[template2] 8/10] ;; posH + Length[template2]]],

-dataLwhitened[[posL + Floor[Length[template2] 8/10] ;; posL + Length[template2]]]}, PlotRange -> All]

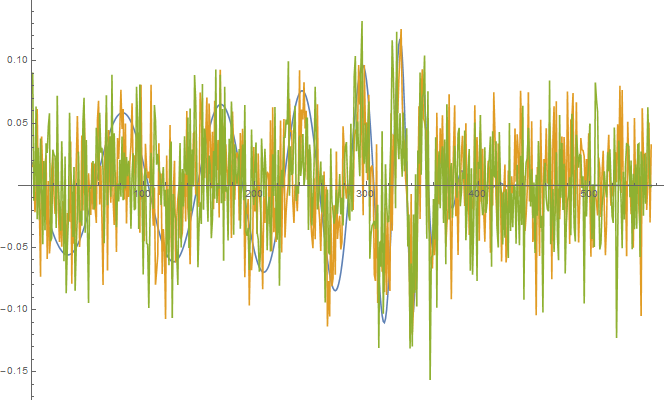高周波のノイズがまだ残っていて、わかりにくいですね。データから10～280Hzの部分だけを取り出してみます。

dataHfiltered =BandpassFilter[dataHwhitened, {10, 280} 2 Pi, 300, HammingWindow,SampleRate -> sr];
dataLfiltered =BandpassFilter[dataLwhitened, {10, 280} 2 Pi, 300, HammingWindow,SampleRate -> sr];
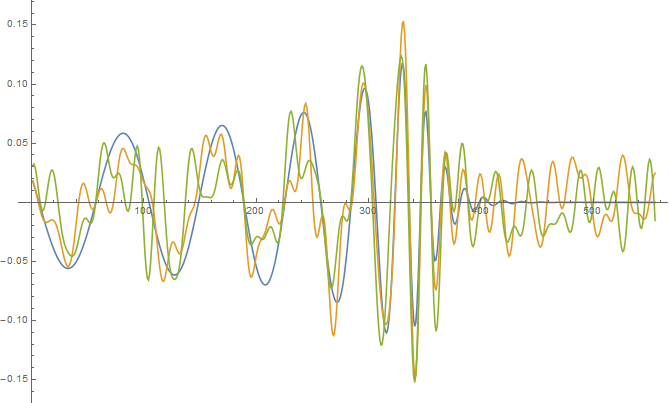
ListLinePlot[Normalize /@ {template2[[Floor[Length[template2] 8/10] ;; Length[template2]]],
dataHfiltered[[posH + Floor[Length[template2] 8/10] ;; posH + Length[template2]]],
-dataLfiltered[[posL + Floor[Length[template2] 8/10] ;;posL + Length[template2]]]}, PlotRange -> All]

かなり良い感じではないでしょうか。というわけで、家庭のコンピュータでも重力波検出は一応可能でした。ただ実際には、もっと多くのパターンとの照合や、突発的なノイズ（地震、周囲の交通、風など）への対応が必要なのでしょう。