スパゲッティの乾麺を折るとなぜ3つ以上に分裂するのか(1)

　最近、スパゲッティの乾麺を折ると3つ以上に分裂することを解明した論文を読んだのですが、いろいろと疑問が湧いてきたので、麺シミュレーションを作ってみました。

（クリックすると動きます。）

　この動画をtwitterに公開したところ、やんぼりさんと議論になりました。それは、1度目の破断が発生する前の形はどうなるのか、ということに関してです。それをずっと考えていたのですが、何とか解らしきものが形になったので、公開したいと思います。

結論から言えば、次の通りです。
・乾麺を曲げた時の形は、力のかけ方によって異なる。
・手首の回転だけでトルクをかけるように曲げた場合は曲率が一定、つまり円形となる。(case1)
・両手で麺を押すように曲げた場合は、中央ほど曲率が高くなる。(case2)
・麺を引っ張るように曲げた場合は、端ほど曲率が高くなる。(case3)
・スパゲッティを折った時に3つ以上に分裂しやすいのは、case1の時。

　この手の問題は、ベルヌーイ・オイラーの梁理論などで解けると思うのですが、微少変位の理論しか見つけられず、スパゲッティのように大きく曲げられる物質には不適当だと判断しました。そこで、車輪の再発明かもしれませんが、スパゲッティ乾麺の折り曲げに特化した式を作ってみました。

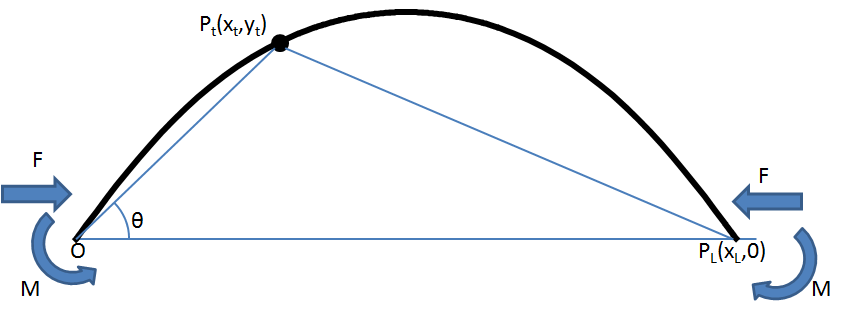
　次のように考えます。両手を$x$軸上に置き、長さ$L$の麺を曲げ、その端の一つを原点、そこを基点に麺上で距離tだけ進んだ位置を$P_t(x_t,y_t)$とします。麺に対する力のかけ方は、2つのパラメータで表現します。麺の両端からかける力$F$と、麺をねじるトルク$M$です。

　点$P_t$が左手から受けるモーメントは、$P_t$から$F$の作用線までの距離$y_t$に$F$を掛け、$M$を加えた$F y_t+M$となります。右手からも同じモーメントを受け、釣り合います。

　さて、弾性曲線方程式によれば、点$P_t$の曲率$\rho_t$は曲げモーメントを$-EI$(曲げ剛性定数)で割った値となります。結局$\rho_t=-\frac{M+F y_t}{EI}$が成り立ち、$M$と$F$を固定すれば$y$座標値だけで曲率が決まります。

　3ケースについて注目したいと思います。（これらに含まれない力の加え方もあります。）

　(case1)$F=0, M>0$とすると、曲率は一定、つまり円形となります。これは、腕の力を抜いて自由に動く状態にし、手首のひねりだけで麺を折ろうとする場合に相当します。この場合、最初の折れるのは、麺のたまたま一番弱い部分なので、破断位置の分布は一様分布になるでしょう。折れた直後の曲率も一定なので、麺が3つ以上に分裂する可能性も高くなります。これは、実際に試しても実感できます。

　(case2)対して$F>0, M=0$とすると、真ん中の曲率が最大になります。これは、麺にひねりを加えずに両側から押さえるように折る場合です。この場合、最初に破断するのは真ん中付近でしょう。麺が3つ以上に分裂する可能性は低くなります。ちなみに微少変位理論で近似すると、麺の形はsinカーブとなります。

　(case3)$F<0, M<0$の場合は、端の曲率が高くなります。麺を横に引っ張りながらひねりも加える折り方で、最初の破断は端の方で発生します。 　何も意識せずに麺を折ると、case1とcase2を合わせたような力のかけ方になるような気がします。また、論文で前提としていたのは曲率一定のcase1なので、妥当な選択だと思います。 　それぞれの場合について、数値計算を実施した結果です。

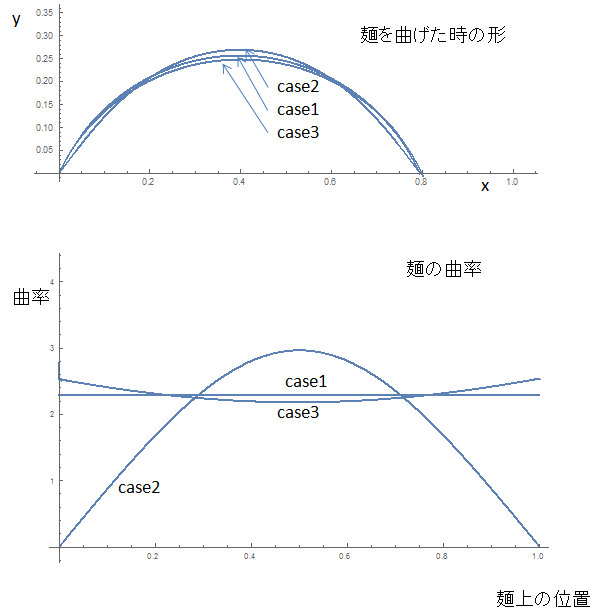
上の曲線は、関数の曲率を表す式を考えて、微分方程式$-\frac{M+F y_t}{EI}=\frac{y”_t}{(1+y’_t)^\frac{3}{2}}$を解けば求められます。この式は常微分方程式なので一応数値計算可能ですが、境界条件が難しいです。$y_0=0$は良いとして、もう一つは弧の長さが$L$になった時点の$y$が0という、少し面倒な式になります。弧の長さを表す変数を用意して微分方程式を連立し、2点境界値問題として解く必要があります。